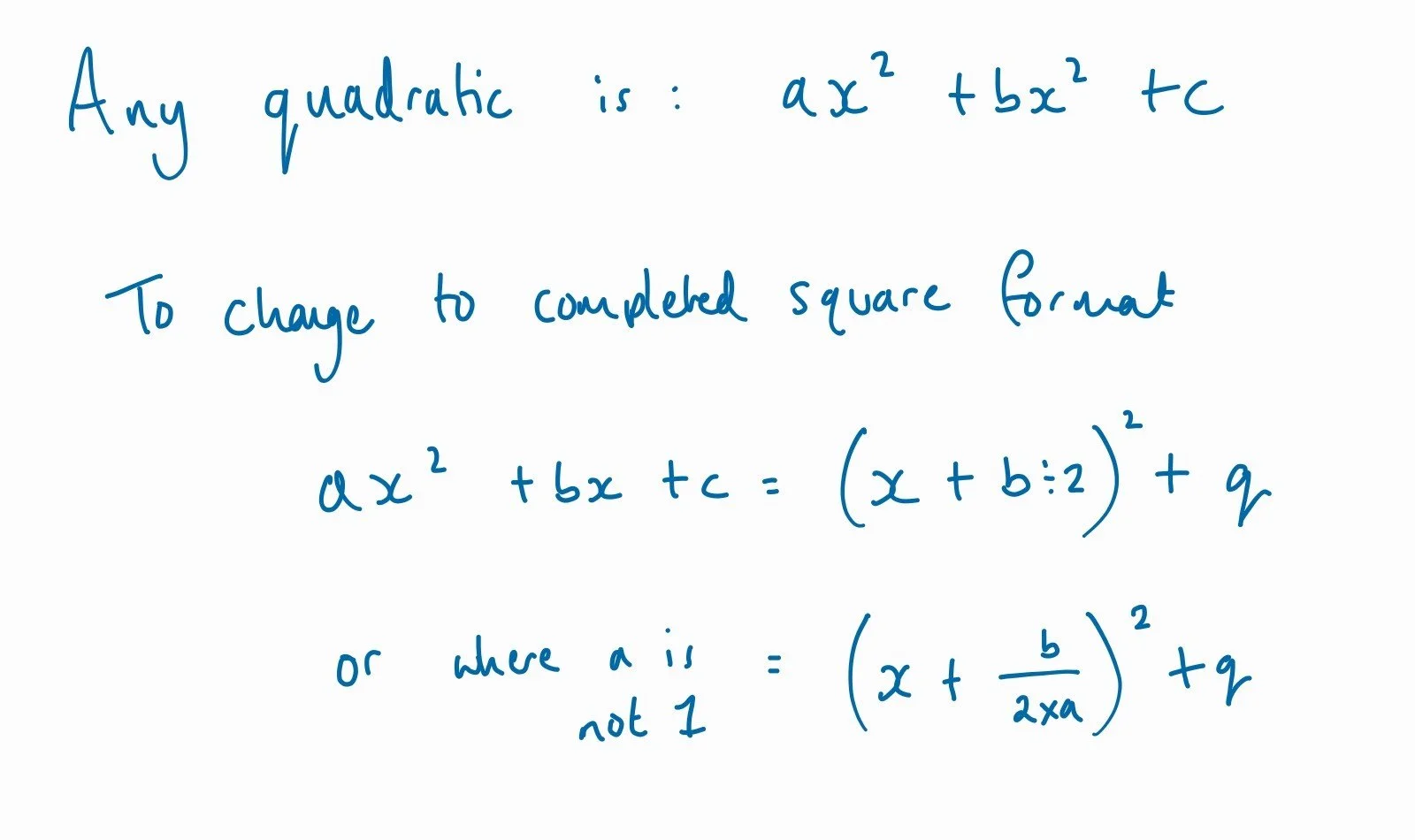The fast way to ‘Complete the Square’ that nobody tells you

Just made a quick video in case you are stuck on completing the square.

With completing the square, it looks and sounds scarier than it is.

What you are doing is rewriting a quadratic in a different form.

So in this example, we want to write x^2 + 4x + 5 in completed square form.

Completing the square is a different way to factorise a quadratic, not all quadratics will factorise with double brackets.

So we use a squared bracket with an additional number - hence the name completing the square.

Here’s another example from the CGP GCSE maths textbook

The above equation can be written as shown on the right.

The video above shows a quicker way to calculate the values.

So how does completing the square help us solve the equation?

Let’s do some examples where we actually solve the equation too.

Tip: It helps if you are at least familiar with surds. I will be also be writing a more detailed blog post on surds soon.

Quiz 1: Write the Equation in Completed Square Form

12345

1. Write the equation x² + 6x + 5 in completed square form

Submit

2. Write the equation x² - 4x + 3 in completed square form

Submit

Well done! You've completed the quiz.

Quiz 2: Solve Equations Using Completing the Square

12345

1. Solve using completing the square: x² + 6x - 7 = 0

Submit

Great job! You've finished the quiz.

Hope that helps!

Will add more examples and practice questions here soon!