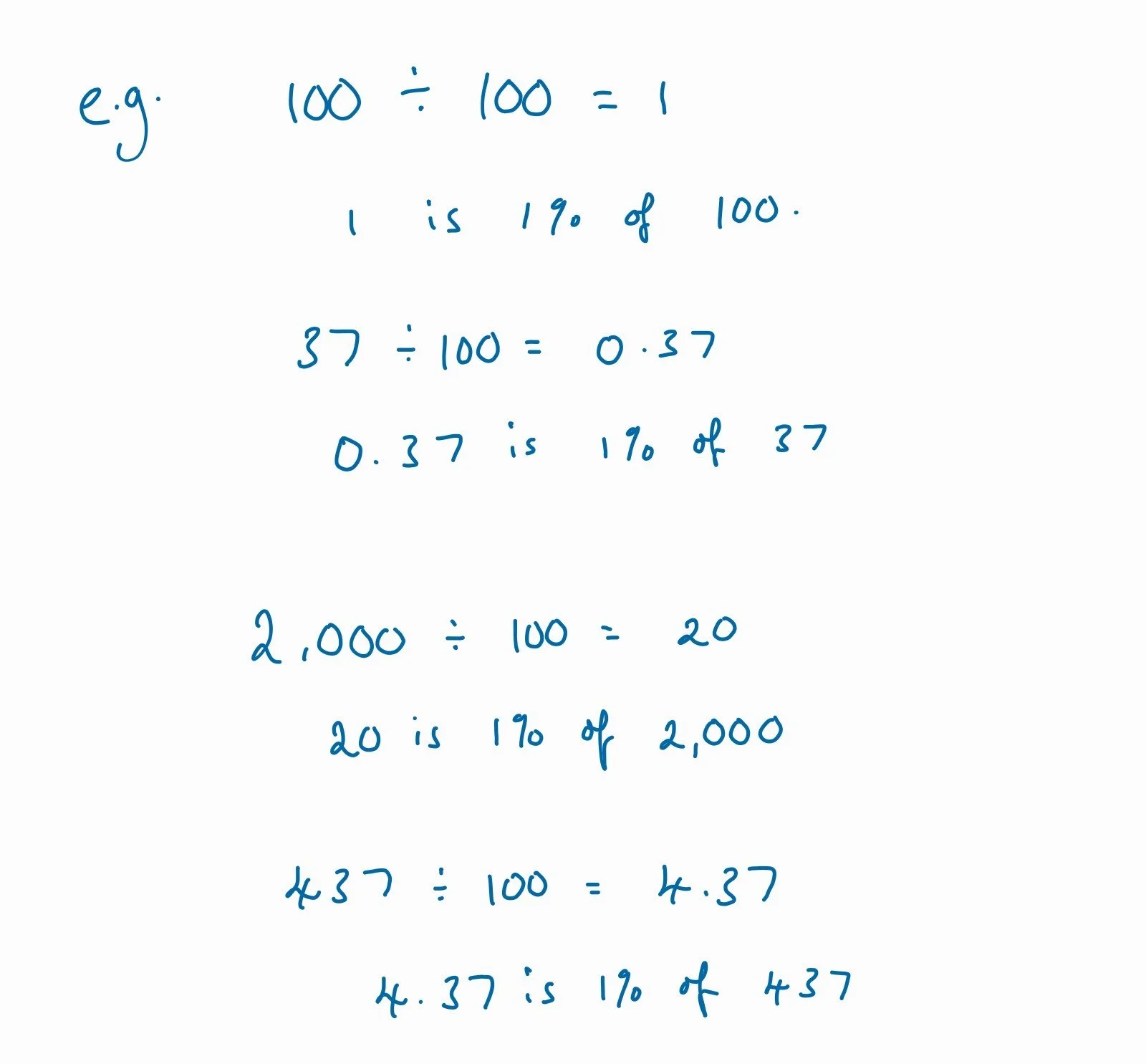Percentage Increase & Decrease - like making your own pop corn
Popcorn. Always 10% bigger than your bowl.
Percent is a big topic in Secondary School Maths. If you don’t fully understand percentages whilst in KS3 - years 7 to 9 - you will struggle a lot in year 10 and 11 whilst preparing for your GCSE maths exam.
By the way, the work you do in years 7, 8 and 9 is the foundation maths GCSE. So, although nobody tells you, you do actually start your maths gcse in year 7.
Also, as I always say, you don’t have to wait for your school or your teacher to tell you what to learn…they usually take ages to cover the topics.
You should learn them as soon as you can, there is no harm in being ahead of your school work… you will have more time for fun and your parents will stop harassing you about your homework - win-win!
In this blog, we will be learning about percentage increase and decrease.
In order to do that you first need to know how to find a percentage of an amount.
We looked at expressing one number as a percentage of another number in this blog post: ‘How to find percent whilst munching on cupcakes’ Here’s a quick recap and some practice questions:
Write or Express one number as a percentage of another
When you do a test, your mark is usually given in 2 ways:
1: Your actual score out of the total possible marks in the exam
2: That score as a percentage.
How are these 2 linked?
Well if you scored 47/50 in your test. You can turn that into a percentage.
A fraction is a divide. So calculate the divide: 47/50 then multiply by 100
Here are some practice questions:
Expressing Numbers as Percents
Finding a percent of a number
So, here we start the juicy bit.
To do an increase or decrease, you need to first be able to find a percent of a number.
What does that mean exactly??
If I say to you: find 25% of 80, you need to be able to work that out.
Don’t panic yet, I will show you some easy ways to do this:.
Method 1: Divide by 100 and then multiply by the percent you want
Because percent is out of 100, dividing a number by 100, always gives you 1% of that number.
Once you’ve found 1% of a number, you can multiply that number to find any percent that you want.
If we want 25% of 37, we know that 1% is 0.37.
0.37 multiplied by 25 is 9.25.
So 25% of 37 is 9.25
Or, if we want to calculate 42% of 2,000:
We know that 1% is 20, 20 multiplied by 42 is: 840.
So 42% of 2,000 is 840.
To increase or decrease a number by a percent, find the percent than simply add or subract.
E.g. Increase 2,000 by 42%.
We know that 42% is 840.
2,000 + 840 is 2,840.
So the answer is 2,840.
Faster Methods To Find Percent
Just like most things, once you understand the long way and the underlying reasons why things work the way they do, you can find shortcuts.
Finding percent in maths, and doing percentage changes is just the same.
If you need to find common percentages, like 25%, 50%, 20%, 75% and so on, you can use their fraction equivalents. For example:
| Fraction | Percentage | Decimal | Divide By | Multiply By |
|---|---|---|---|---|
| 1/2 | 50% | 0.5 | 2 | 0.5 |
| 1/3 | 33.33% | 0.333 | 3 | 0.333 |
| 1/4 | 25% | 0.25 | 4 | 0.25 |
| 1/5 | 20% | 0.2 | 5 | 0.2 |
| 1/6 | 16.67% | 0.167 | 6 | 0.167 |
| 1/8 | 12.5% | 0.125 | 8 | 0.125 |
| 1/10 | 10% | 0.1 | 10 | 0.1 |
| 1/12 | 8.33% | 0.083 | 12 | 0.083 |
| 1/16 | 6.25% | 0.0625 | 16 | 0.0625 |
| 1/20 | 5% | 0.05 | 20 | 0.05 |
| 1/25 | 4% | 0.04 | 25 | 0.04 |
| 1/50 | 2% | 0.02 | 50 | 0.02 |
| 1/100 | 1% | 0.01 | 100 | 0.01 |
You can divide to find the percentage of a number, or multiply by its decimal equivalent.
The link between Percentages, Fractions and Decimals
You need to know how to convert between decimals, percentages and fractions.
Remember, they all represent the same thing, just in a different format. A bit like saying: “Hi”, “Hello”, “Hey”. They all mean the same thing, just expressed differently.
Percent Increase & Decrease
And Finally…now that you know everything about finding a percent of a number, you can increase or decrease a number by a percent.
Step 1: Find the percent you need.
Step 2: Add or subtract that number from the original amount.
E.g. Increase 20 by 10%.
10% of 20 is 2 (divide by 10). So to increase, we add 2 to 20. The answer is 22.
This method is great for non calculator questions.
If you have a calculator question, there is a faster method:
Use a multiplier.
E.g. if you want to increase something by 50%, what you are saying is you want that whole thing, with 50% added. Its like saying I want a whole cake and then 50% of a second cake - no problem, cake is good.
Now, 1 and another half of a cake (or anything) is the same as 1.5, or 150%.
So you can just mulitply the original number by 1.5.
E.g. increase 20 by 50%.
Do 20 x 1.5 and this will give you 30.
Because half of 20 is 10, so increasing 20 by 50% is 30.
You can do this for any percentage increase by adding the decimal version of that percentage to 1.
E.g. to increase by 20%, multiply by 1.20
Increase by 37%, multiply by 1.37
Increase by 62%, multiply by 1.62
And so on.
Percentage decrease is slightly different, you will need to subtract from from 1.
E.g. Decrease 20 by 10%, means that you want 90% of that number. The decimal version of 10% is 0.1.
So you multiply by 1 - 0.1 = 0.90
0.90 x 20 = 18.
Decrease 20 by 50%, multiply by 1 - 0.5 = 0.5
Decrease 20 by 30%: 1 - 0.3 is 0.7 so do 0.7 x 20 = 14.
And so on.
Hope that helps :)
Please share to your network if you found this useful.