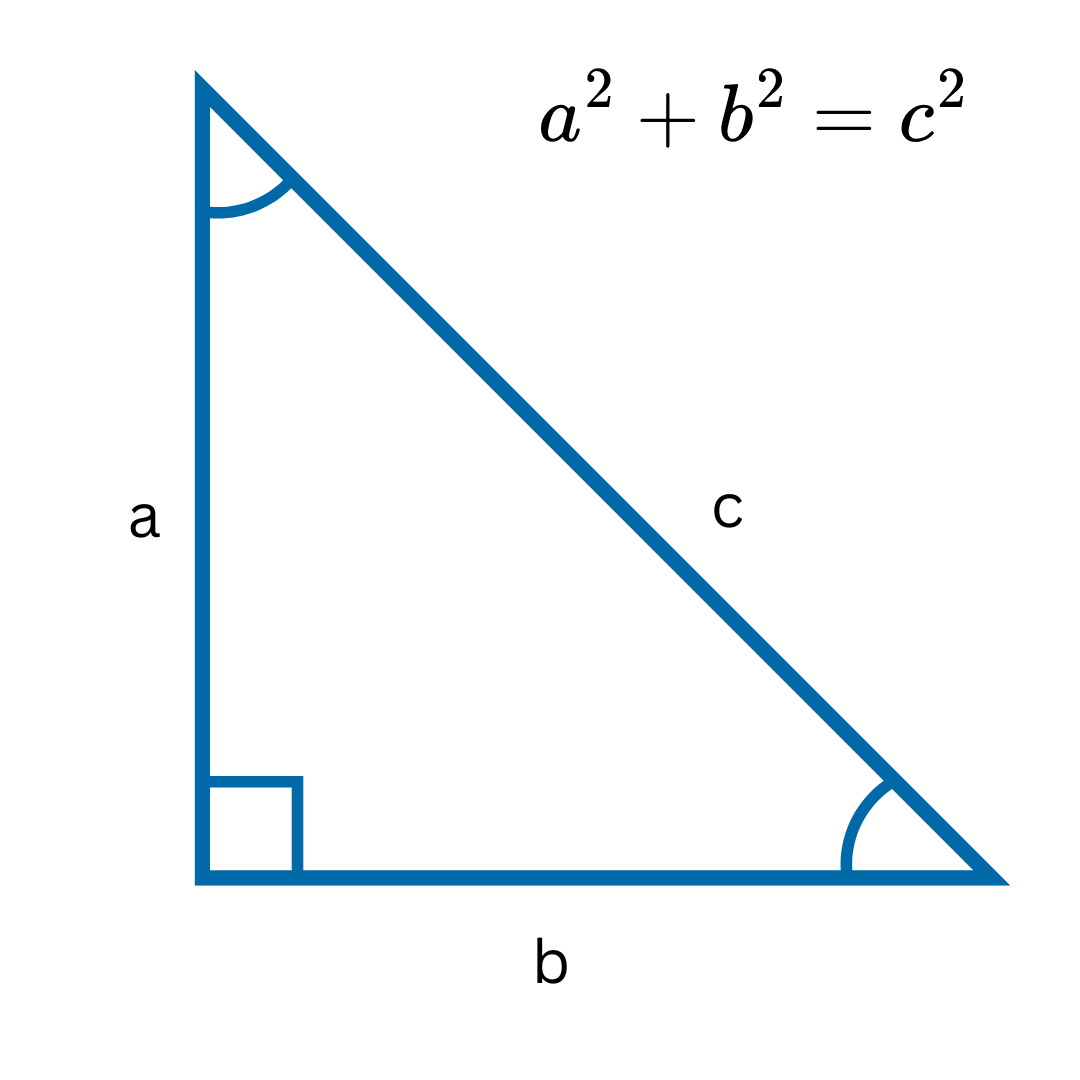How to do sin, cos, tan and use the right one in the exam

I know this is your favourite topic, definitely what you want to spend your free time on a Sunday evening doing…ok, maybe not, but I’m hoping to make it painless enough for you to understand and get some easy marks in the exam.

This post is going to be all about Trigonometry, I will be starting with pythagoras, which isn’t really trig, but you need to know it to do the rest.

What is Pythagoras?

Pythagoras is a really cool concept that describes the link between the 3 sides of a right angled triangle.

It looks like this:

Note: You might see it with a h instead of the c

The hypotenuse is the longest side of a right angled triangle and its always the side opposite the right angle.

Here’s a reminder of angles:

With pythagoras, you can work out how long one side of a triangle is, as long as you have the lengths of the other 2 sides.

There are two types of pythagoras questions that usually come up. 1 is where they give you the lengths of a and b and you have to work out the length of c or the hypotenuse.

The other way they ask the question is to give you the length of the hypotenuse (which is also c) and the length of one of the shorter sides. To answer these you have to rearrange the formula and subtract the squared sides from each other:

Worked Examples of Pythagoras Theorem

Example 1:

Question: A right-angled triangle has a base of 6 cm and a height of 8 cm. Find the length of the hypotenuse.

Solution:

The formula for Pythagoras' theorem is:

c² = a² + b²

Where:

• c is the hypotenuse,
• a and b are the other two sides.

Substitute the values:

c² = 6² + 8²
c² = 36 + 64
c² = 100

Taking the square root of both sides:

c = √100 = 10 cm

Final Answer: The hypotenuse is 10 cm.

Example 2:

Question: A right-angled triangle has a hypotenuse of 13 cm and one side of 5 cm. Find the length of the other side.

Solution:

Rearrange the Pythagoras' theorem to solve for one side:

b² = c² - a²

Substitute the values:

b² = 13² - 5²
b² = 169 - 25
b² = 144

Taking the square root of both sides:

b = √144 = 12 cm

Final Answer: The other side is 12 cm.

Pythagoras Theorem Quiz

1. A right-angled triangle has a base of 5 cm and a height of 12 cm. Find the length of the hypotenuse.

2. A triangle has a hypotenuse of 25 cm and one side of 24 cm. Find the length of the other side.

3. In a right-angled triangle, the base measures 7 cm and the hypotenuse measures 10 cm. Find the height of the triangle.

4. A ladder leans against a wall. The base of the ladder is 9 m from the wall, and the ladder reaches a height of 12 m. How long is the ladder?

5. A square has a diagonal length of 13 cm. Find the length of one side of the square.

Trig for Right-Angled Triangles

Pythagoras helps you find the length of a side in a right angled triangle.

Its great if you have 2 side lengths.

What if you only have 1 side length and an angle - other than the right angle.

This is where Trigonemetry comes in.

What is trigonmetry or trig?

In very simple terms trig works out the ratio between the angles and the lengths of the sides.

Those ratios are worked out with Trig Functions called Sine, Cosine and Tan.

Here’s how it works.

In a right angled triangle, the smaller angles are linked to the lenghs of 2 of the other sides.

It could be the opposite side to the angle and the hypotenuse. Use Sine.

It could be the adjacent (side that is next to the angle) and the hypotenuse. Use Cosine.

It could be the opposite and the adjacent side. Use Tan.

How do you know which sides to choose?

It depends on the question.

Trig questions involve 3 things: an angle, the length of 2 sides.

You may have come across the word: SOH CAH TOA this is to help you know which function to use.

Here are some examples to help you understand.

In the triangle above we want to find the length of the side labelled ‘a’.

We have 2 pieces of information, the size of the angle which is 36 degrees and the length of the hypotenuse which is 12cm.

Side ‘a’ is opposite the 36 degree angle.

So the sides we are looking at are the hypotenuse ‘H’ and the opposite side ‘O’

If you look at the SOH CAH TOA phrase, the part with H and O is the SOH part.

This means we need to use sine.

The SOH also tells us the formula: sin x = opp/hyp

So fill in the numbers that we know: sin 36 = a/12

We want a on its own, so rearrange (tip, if you struggle with solving equations, this bit might confuse you, go back and practice your algebra!!)

12 sin 36 = a

Using a calculator we get: 7.05342..

So 7.05 to 2 dp or 7cm to a whole number.

Trigonometry Example: Cosine

Question: A ladder leans against a wall, forming an angle of 60° with the ground. The bottom of the ladder is 4 meters away from the wall. How long is the ladder?

Solution:

We can use the cosine ratio:

cos(θ) = Adjacent / Hypotenuse

Here:

• θ = 60°
• Adjacent side = distance from the bottom of the ladder to the wall = 4 meters
• Hypotenuse = length of the ladder (let's call it L)

Using the formula:

cos(60°) = 4 / L

Steps to Solve:

1. From trigonometric tables or a calculator, cos(60°) = 0.5.
2. Substitute into the equation: 0.5 = 4 / L
3. Rearrange to solve for L: L = 4 / 0.5 = 8

Final Answer:

The ladder is 8 meters long.

Trigonometry Example: Tangent

Question: A tree casts a shadow that is 15 meters long. The angle of elevation from the tip of the shadow to the top of the tree is 30°. How tall is the tree?

Solution:

We can use the tangent ratio:

tan(θ) = Opposite / Adjacent

Here:

• θ = 30°
• Adjacent side = length of the shadow = 15 meters
• Opposite side = height of the tree (let's call it h)

Using the formula:

tan(30°) = h / 15

Steps to Solve:

1. From trigonometric tables or a calculator, tan(30°) ≈ 0.577.
2. Substitute into the equation: 0.577 = h / 15
3. Rearrange to solve for h: h = 15 × 0.577 ≈ 8.66

Final Answer:

The tree is approximately 8.66 meters tall.

Trigonometry Quiz

Answer the following questions. Click "Show Worked Answer" for help!

This isn’t finished yet - will be adding more info and example questions this week